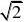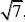上海市闵行区2010届高三上学期期末质量调研考试(数学理)
上海市闵行区2010届高三上学期期末质量调研考试数 学 试 卷(理科)考生注意:1.答卷前,考生务必在答题纸上将学校、姓名及准考证号等填写清楚,并在规定的区域内贴上条形码.答题时客观题用2B 铅笔按要
上海市闵行区2010届高三上学期期末质量调研考试
数 学 试 卷(理科)
考生注意:
1.答卷前,考生务必在答题纸上将学校、姓名及准考证号等填写清楚,并在规定的区域
内贴上条形码.答题时客观题用2B 铅笔按要求涂写,主观题用黑色水笔填写.
2.本试卷共有23道题,共4页. 满分150分,考试时间120分钟.
3.考试后只交答题纸,试卷由考生自己保留.
一. 填空题(本大题满分56分)本大题共有14题,考生应在答题纸上相应编号的空格内
直接填写结果,每个空格填对得4分,否则一律得零分.
1

.函数f (x ) 1的反函数f -1(x ) = .
2n 2-1= . 2.lim 2n →∞n n
3.从一堆苹果中任取5只,称得它们的质量分别为(单位:克)125、124、122、123、
126,则该样本方差s 2= .
4.已知集合A ={x x -2<3, x ∈R },
B ={x 2x >2a , x ∈R },A ,且A B =那么实数a 的取值范围是 . 3215.化简行列式x y z = . -1106.在右面的程序框图中,要求输出三个实数a 、b 、c 中 最大的数,则在空白的判断框中应填的是 . 7.某校高二(8)班4位同学的数学期中、期末和平时成


⎛95⎫⎛88⎫⎛90⎫ ⎪ ⎪ ⎪908592⎪ ⎪ ⎪ 绩依次用矩阵A =表示, 、B =、C = 80⎪ 76⎪ 78⎪ ⎪ ⎪ ⎪7583⎝⎭⎝⎭⎝60⎭
总评成绩按期中、期末和平时成绩的30、40、30的
总和计算,则4位同学总评成绩的矩阵X 可用A 、B 、C
表示为 .
8.如图,直三棱柱OAB -O 1A 1B 1中,∠AOB =90,M 是

侧棱BB 1上一点,向量a =(1, 1, -1)是平面OA 1M 的一
个法向量,则平面OAB 与平面OA 1M 所成二面角的锐角
为 (结果用反三角函数值表示).
9.已知函数f (x ) =lg 1-x sin x 1. 若f (m ) =4,则f (-m ) = . 1 x
10.在平面直角坐标系xOy 中,以Ox 轴为始边作两个锐角α、β,它们的终边分别与单位圆相交于A 、B 两点,若A 、B 两点的横坐标分别为54β⎫⎛、. 则tan α ⎪的值为 . 1352⎭⎝
1000π

cm 3. 311.用铁皮制作一个无盖的圆锥形容器,已知该圆锥的高为10cm ,体积为
2则制作该容器需要铁皮面积为 cm 1.414,
π取3.14,结果保留整数).
12.已知无穷数列{a n },首项a 1=3,其前n 项和为S n ,且a n 1=(a -1) S n 2 8(a ≠0, a ≠1, n ∈N *) . 若数列{a n }的各项和为-a ,则a = . 3
13.如图,△ABC 中, AB =4, AC =8, ∠BAC =60 ,
延长CB 到D ,使BA =BD ,当E 点在线段AD
上移动时,若=λ μ,则t =λ-μ
,的最大值是 .
14

.设函数f (x ) =(a <0) 的定义域为D ,
若所有点(s , f (t ))(s , t ∈D ) 构成一个正方形区域,则a 的值为 .
二. 选择题(本大题满分16分)本大题共有4题,每题只有一个正确答案. 考生应在答题
纸的相应编号上,将代表答案的小方格涂黑,选对得4分,否则一律得零分.
15.“11 (A) 充分非必要条件. (B) 必要非充分条件. (C) 充要条件. (D) 既非充分亦非必要条件. 16.函数y =f (x ) 的图像与y =ln(x -2) 的图像关于x =1轴对称,若f (a ) =-1,则a 的 值是 [答]( ) (A) -e . (B) e . (C) -. (D) 1 e 1. e 17.2010年上海世博会要从小张、小赵、小李、小罗、小王五名志愿者中选派四人分别从 事翻译、导游、礼仪、司机四项不同工作,则小张不从事翻译工作且小赵不从事司机工作的概率是 [答]( ) (A) 319213. (B) . (C) . (D) . 205205 18. 在平面直角坐标系中,定义⎨⎧x n 1=y n -x n ⎩y n 1=y n x n (n ∈N )为点P (x , *n n y n ) 到点 P n 1(x n 1, y n 1) 的一个变换,我们把它称为点变换. 已知P 1(0, )1,P 2(x 2, y 2), , P n (x n , y n ), P n 1(x n 1, y n 1)(n ∈N *)是经过点变换得到的一列点. 设a n =P n P n 1,数列{a n }的前n 项和为S n ,那么lim (A) S n 的值为 [答]( ) n → ∞a n (B) 2 (C) 2 (D) 1三. 解答题(本大题满分78分)本大题共有5题,解答下列各题必须在答题纸相应编号的规定区域内写出必要的步骤. 19. (本题满分14分) 已知四棱锥P -ABCD , PA ⊥底面D A B C , PA D =1,底面ABCD 是正方形,E 是PD 的中点,PD 与底面ABCD 所成角的大小为π,求异面直线AE 与PC 所成角的大小(结果6 用反三角函数值表示). B 20. (本题满分14分)本题共有2个小题,每小题满分各7分. 已知以角B 为钝角的∆A B C 的内角A 、B 、C 的对边分别为a 、b 、c , m =( a , 2b ), n =-sin A ,且⊥. ) (1)求角B 的大小; (2)求cos A cos C 的取值范围. 21. (本题满分16分)本题共有2个小题,每小题满分各8分. 某公园举办雕塑展览吸引着四方宾客. 旅游人数x 与人均消费t (元)的关系如下: ⎧-12t 1600(10≤t ≤50, t ∈N ); x =⎨-6t 1300(50 (1)若游客客源充足,那么当天接待游客多少人时,公园的旅游收入最多? (2)若公园每天运营成本为5万元(不含工作人员的工资),还要上缴占旅游收入20的税收,其余自负盈亏. 目前公园的工作人员维持在40人. 要使工作人员平均每人每天的工资不低于100元,并维持每天正常运营(不负债),每天的游客人数应控制在怎样的合理范围内? (注:旅游收入=旅游人数×人均消费) 22. (本题满分16分)本题共有3个小题,第1小题满分4分,第2、3小题满分各6分. 已知等差数列{a n }中,公差d >0,其前n 项和为S n ,且满足a 2⋅a 3=45, a 1 a 4=14. (1)求数列{a n }的通项公式; (2)设由b n =S n 1(c ≠0)构成的新数列为{b n },求证:当且仅当c =-时,数n c 2 列{b n }是等差数列; (3)对于(2)中的等差数列{b n },设c n =8*(n ∈N ),数列{c n }的前 (a n 7) ⋅b n ⎫n *, ⎪⋅0.9(n ∈N )⎭⎛8f (n ) =T ⋅a 3-n 项和为T n ,现有数列{f (n ) }, n n b n ⎝ *是否存在整数M ,使f (n ) 值,若不存在,请说明理由. 23. (本题满分18分)本题共有3个小题,第1小题满分4分,第2小题满分8分,第3 小题满分6分. 已知函数f (x )=log a (x 1)(a >1),函数g (x )的图像与函数y =32(a >1)的图像关于直线y =x 对称. (1)求函数g (x )的解析式; (2)若函数g (x )在区间[m , n ] m > 求实数p 的取值范围; (3)设函数F (x )=a f (x )-g (x )(a >1),试用列举法表示集合M =x F (x )∈Z . ⎛⎝3⎫⎪上的值域为[log a (p 3m ), log a (p 3n )], 2⎭{} 闵行区2009学年第一学期高三年级调研考试 数学试卷参考答案和评分标准 一、填空题(每题4分) 1. (x -1); 3 2. 2; 3. 2; 4. (-∞, -1]; 5. x y -5z ; 6. 理a >b 且a >c ? ;文b >c ? ; 7. 0. 3A 0. 4B 0. 3C ;8. 理10. 理;文 9. -2; 411;文2; 11. 444; 12. 理-;文-2; 23 13. 理1 ;文 2; 14 -4. 二、选择题(每题4分) 15. A ; 16. C ; 17. B ; 18. C 三、解答题(19题至23题)19. (本题满分14分) (理科) 取CD 中点F ,连AF , E 为PD 中点,∴EF //PC , ∴∠AEF (或其补角)的大小即为异面直线AE 与PC 所成的角的大小, (2分) PA ⊥底面ABCD ,∴∠PDA 就是PD 与底面ABCD 所成角,即∠PDA = 且PA ⊥AD , PA ⊥AC ,由已知条件及平面几何知识,得:PD = 2, π6, AD ==AB AE =1AC =AF = PC =EF =(8分) 12 22-= (12分) 在∆ AEF 中,由余弦定理得:cos ∠AEF = ∴∠AEF =π-, 即异面直线AE 与PC 所成的角的大小为arccos . (14分) 7 另解: 以A 为原点,分别以AB 、AD 、AP 所在直线为x 、y 、z 轴建立空间直角坐标系, PA ⊥底面ABCD ,∴∠PDA 就是PD 与底面ABCD 所成角,即∠PDA =PA ⊥AD , PA ⊥AC ,由已知条件及平面几何知识,得: π6,且 PD =2, AD ==AB , ∴A (0,0,0), P ( 0,0,1), C ⎛1⎫ ∴AE = 2⎪⎪,PC = ⎝⎭ ⎛1⎫, E 2⎪⎪ (4分) ⎝⎭)-1 (8分) ) AE PC =∴cos θ=, (12分) =AE PC 即异面直线AE 与PC 所成的角的大小为. (14分) (文科)取BC 中点E ,连AE , DE , D 为PC 中点,∴DE //PB , ∴∠ADE (或其补角)的大小即为异面直线AD 与PB 所成的角的大小. (2分) PA ⊥底面ABC ,∴∠PCA 就是PC 与底面ABC 所成角,即∠PCA = PA ⊥AB , PA ⊥AC ,由已知条件及平面几何知识,得: π6,且 PC =2, AC =AB =, PB =2,于是AD =1, DE =1, AE =6, (8分) 2 6 AD 2 DE 2-AE 2=1(12分) 在∆ADE 中,由余弦定理得cos ∠ADE ==2AD ⋅DE 2⨯1⨯14 11∴∠ADE =arccos ,即异面直线AD 与PB 所成的角的大小为arccos .(14分) 441 1- 20. (本题满分14分)(1)⊥. ∴m ⋅n =0-2b sin A =0 (2分) 由正弦定理,得a =2R sin A , b =2R sin B ,代入得: (3分) sin A -2sin B sin A =0,sin A ≠0,∴sin B = B 为钝角,所以角B =3, ( 5分) 22π. (7分) 3 A C A -C πcos =C -) 226(2)(理科) cos A cos C =2cos (或:cos A cos C =cos A cos ⎛π⎫-A ⎪ ⎝3⎭13π⎫⎛=cos A cos A sin A =sin A ⎪) (10分) 223⎭⎝ π⎫⎛⎤π⎛π2π⎫⎛⎛π⎫ , 1⎥ (12分) 由(1)知 A ∈ 0, ⎪, A ∈ , ⎪, ∴sin A ⎪∈ 323333⎝⎭⎝⎝⎭⎝⎭⎦ 故cos A cos C 的取值范围是 ⎛3 (14分) ⎝2(文科) sin A A =2sin A ⎛ ⎝π⎫⎪, (10分) 3⎭ π⎫⎛⎤π⎛π2π⎫⎛⎛π⎫ , 1⎥,由(1)知 A ∈ 0, ⎪, A ∈ , (12分) ⎪,∴sin A ⎪∈ 323333⎝⎭⎝⎝⎭⎝⎭⎦ 故sin A 3cos A 的取值范围是3, 2] (14分) t 5N ∈0, ) (4分) 2t 0N ∈0, ) 21. (本题满分16分)(1)设当天的旅游收入为L ,那么L=xt,得 ⎧-12t 2 160t 0, (≤1t 0≤⎪ L =⎨25t 0≤⎪⎩-6t 130t 0, (< 22当10≤t ≤50时, L =-12t 1600t ≤-12⨯50 1600⨯50=50000(元) (5分) ⎛325⎫211250当50 t ∈N , ∴当t =108元时,L max =70416(元) (6分) 此时 x =652(人) (7分) 故当天接待旅游人数为652人时旅游收入最多,收入为70416元. (8分) (2)要使工作人员平均每人每天的工资不低于100元,并维持每天正常运营,即每天的旅游收入上缴税收后不低于54000元, 因-12t 1600t ( (2)max =50000≤54000, (10≤t ≤50), 显然不满足条件 (10分) 22由-6t 1300t ⨯80≥54000⇒3t -650t 33750≤0(50 0 (14分) 得 87≤t ≤13. 因此520≤x ≤778,故每天的游客人数应控制在520人到778人之间. (16分) 22. (本题满分16分)(1)∵等差数列{a n }中,公差d >0, ∴⎨⎧a 2⋅a 3=45⎧a 2⋅a 3=45⎧a 2=5⇒⎨⇒⎨⇒d =4⇒a n =4n -3 (4分) ⎩a 1 a 4=14⎩a 2 a 3=14⎩a 3=9 n (1 4n -3)n (2n -1)S =n (2n -1),b n =n =, (6分) n c 2n c (2)S n = 由2b 2=b 1 b 3得121151= ,化简得2c 2 c =0, c ≠0,∴c =-(8分) 2 c 1 c 3 c 2 1反之,令c =-,即得b n =2n ,显然数列{b n }为等差数列, 2 1∴ 当且仅当c =-时,数列{b n }为等差数列. (10分) 2 (3)(理科) c n = ∴T n =1-8111 ==-a 7⋅b n 1n n n 1n n 11111n - -= 223n n 1n 1 ⎛8⎫n n ⎛4⎫f (n )=T n ⋅ a n 3-⎪⋅0.9=⋅ 4n -⎪⋅0.9n =4(n -1)⋅0.9n (12分) n 1⎝n ⎭b n ⎭⎝